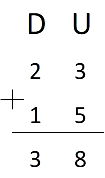2ºB - SUBTRAÇÃO

 A subtração associa-se às ideias de tirar, comparar e completar.

A subtração é uma entre as quatro operações básicas da matemática, sendo aprendida após a adição. Considerada a operação inversa da adição, a subtração entre dois números é representada pelo símbolo – (menos) entre os números, por exemplo 9 – 5 (lê-se: nove menos cinco).

Calcular a subtração é calcular o valor encontrado quando retiramos o subtraendo, ou seja, no exemplo citado, trata-se de quanto resta se retirarmos 5 de 9. Para calcular a subtração entre números maiores, utilizamos o algoritmo da subtração. Além disso, a subtração possui propriedades importantes.

• 
  Resumo sobre subtração
  A subtração é uma entre as quatro operações básicas da matemática.
  Para calcular a subtração entre números maiores, utilizamos o algoritmo da subtração.
  A subtração possui o 0 como elemento neutro.
  O que é a subtração?

  A subtração é considerada uma operação básica da matemática, com a adição, a multiplicação e a divisão. Calcular a subtração entre dois números é diminuir certa quantia de outra já existente. Por exemplo, se existem 8 pessoas em um elevador, e 3 delas descem dele, então, para calcular a quantidade de pessoas restantes, usamos a subtração entre 8 e 3, ou seja, 8 – 3. Se retirarmos 3 de 8, encontraremos o número restante de pessoas no elevador, que são 5.

  Elementos da subtração

  Cada termo da subtração recebe um nome. Calculamos a subtração entre o minuendo, que é a quantia já existente, e o subtraendo, que é a quantidade retirada do minuendo. O resultado da subtração é conhecido como diferença:

  Exemplo:

  8 → minuendo
  3 → subtraendo
  5 → diferença

  Como fazer a subtração

  Para realizar a operação de subtração entre dois números, basta lembrar que ela é a operação inversa da adição e usar a operação inversa para encontrar a resposta. Como vimos, sabemos que 8 – 3 é 5, porque 3 + 5 = 8. Para números menores, esse raciocínio é sempre eficiente.

  Exemplo:

  • 9 – 8 = 1, pois 8 + 1 = 9

  • 12 – 5 = 7, pois 5 + 7 = 12

  • 10 – 4 = 6, pois 6 + 4 = 10

  Para casos em que os números são maiores, é conveniente utilizar o algoritmo da subtração.

• 8 – 3 = 5

• Minuendo

• Será a quantidade da qual partiremos dentro da operação aritmética da subtração, ou seja, o valor numérico do qual se retira outro valor numérico (o subtraendo) para achar o resultado ou diferença.

• Subtraendo

  É a quantidade que será subtraída, ou seja, retirada. Na operação aritmética da subtração este será o valor numérico que deverá ser retirado do outro (minuendo) para encontrar o resultado ou a diferença.

• Algoritmo da subtração

  Quando não for possível encontrar a diferença entre dois números de forma direta, como nos exemplos anteriores, recorremos ao algoritmo da subtração. Vejamos o passo a passo para calcular a subtração entre dois números utilizando o algoritmo.

  Exemplo 1:

  Calcularemos a subtração 84 – 21.

  1º passo: primeiro vamos montar o algoritmo colocando unidade em baixo de unidade e dezena em baixo de dezena, como na imagem a seguir:

  

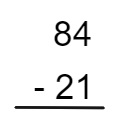
  2º passo: agora calcularemos a diferença, primeira
  mente, entre as unidades, ou seja, 4 – 1, que é igual a 3. O resultado da subtração será escrito logo abaixo da unidade: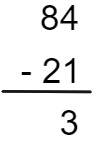

  

  3º passo: por fim, faremos a subtração entre as dezenas, 8 – 2 = 6 dezenas. Então, escreveremos o resultado da seguinte maneira:

  

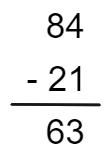
  Assim, temos que: 84 – 21 = 63.

  Exemplo 2:

  Calcule a diferença entre 225 e 34.

  1º passo: montar a diferença no algoritmo.

  

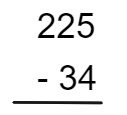
  2º passo: calcular a diferença entre as unidades, 5 – 4 = 1.

  

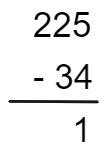
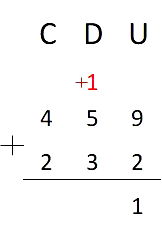
  3º passo: calcular a diferença entre as dezenas, mas note que 2 é menor que 3, então, nesse caso, vamos transformar uma centena em dezena:

  

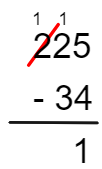
  Agora é possível calcular a diferença entre 12 e 3, 12 – 3 = 9:

  

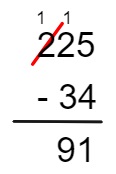
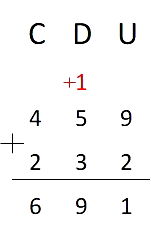
  4º passo: como não há centena no subtraendo, então, basta copiar a centena na diferença.

  

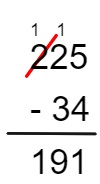
  Assim, temos que 225 – 34 = 191.

https://br.smartick.com/blog/matematica/adicao-e-subtracao/subtracao/ 

2ºB - ADIÇÃO II

 

A adição é o ato de juntar elementos, uma das quatro operações básicas da aritmética. A adição está ligada a ideia de acrescentar. Toda vez que unimos novos elementos ou valores, estamos adicionando.

Em Matemática utiliza-se a símbolo + para representar uma adição.

Termos da adição

Cada elemento somado é chamado parcela. Uma adição pode ter pelo menos duas parcelas e até infinitas.

Exemplo

Ao juntar 300 gramas de arroz com 200 gramas de feijão, temos um prato com 500 gramas.

As parcelas são 300 e 200 e ao resultado, chamamos total ou soma. No exemplo, o resultado 500 é o total ou, a soma.

Conta de somar: cálculo da adição

Também conhecida como conta de mais ou, conta de somar, é um procedimento que nos ajuda a calcular. Este algoritmo da adição é muito útil, principalmente para adições com muitas parcelas ou valores grandes.

Ao efetuar uma adição, escrevem-se as parcelas umas sobre as outras, como uma “pilha” de parcelas e abaixo é feito um traço.

Realizamos a adição somando os algarismos com mesma ordem, começando pelas unidades. Após seguimos somando os algarismos, ordem por ordem.

Exemplo

23 + 15 = 38

Ao escrever os números, estes devem ser organizados colocando ordens iguais em uma mesma coluna. Unidades sobre unidades, dezenas sobre dezenas e assim por diante.

Adição com reserva ou reagrupamento

A Adição com reserva ou reagrupamento também é conhecida como: "vai um”, "vai dois" ... . Ao somar os algarismos em uma ordem, caso o resultado seja maior que 9, devemos acrescentar esta quantidade à ordem seguinte.

Lembre que não podemos escrever mais de um algarismo por ordem.

Exemplo

459 + 232 =

Na ordem das unidades temos 9 + 2 = 11. O número 11 pode ser escrito como 1 dezena + 1 unidade:

11 = 10 + 1

Esta dezena deve ser adicionada à coluna das dezenas.

Na coluna das dezenas temos +1 dezena que será acrescentada ao 5 e ao 3. Como 1 + 5 + 3 = 9, não é necessário acrescentar uma centena e assim, seguimos o cálculo.

Este procedimento deve ser repetido em qualquer ordem caso a soma seja maior que 9. Ao completar uma ordem seguinte, devemos sempre acrescentá-la na coluna correta.

Propriedades da adição

A operação de adição com números naturais possui cinco propriedades e, no conjunto dos números inteiros há uma. Estas propriedades definem a adição e ajudam a calcular.

Propriedade Associativa

Podemos associar as parcelas de modo a facilitar o cálculo.

Exemplo

8 + 6 + 2 + 3= 19

Podemos associar as parcelas da seguinte forma:

8 + 2 + 6 + 3 = 19

10 + 9 = 19

Propriedade Comutativa

A ordem das parcelas não altera a soma.

12 + 3 = 15, assim como, 3 + 12 = 15.

Elemento neutro

O elemento neutro da adição é o zero, pois não altera o resultado.

Exemplos

5 + 0 = 5

4 + 0 + 5 = 9

0 + 37 = 37

Fechamento

A propriedade do fechamento define que ao somar dois ou mais números naturais, o resultado será sempre um número natural.

Exemplo

1 457 + 2 354 = 3 811

Lembre que o conjunto dos números naturais começa com o zero e vai ao infinito, avançando a cada uma unidade.

N = {0,1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, …}

Propriedade do elemento oposto ou simétrico

No conjunto dos números inteiros há a propriedade do elemento oposto ou simétrico, em que um número é oposto ou simétrico quando seu sinal é trocado. Ex.: O oposto ou simétrico de 2 é -2.

Curiosidade: os símbolos de + e -

Os símbolos de adição +, e subtração -, aparecem pela primeira vez na história em 1498, registrados no livro Aritmética Comercial, do alemão Johannes Widmann. Muito embora eram usados para representar excessos e déficits de mercadorias.

Em 1557 o inglês Robert Recorde em sua obra, Whetstone of Witte, empregou estes símbolos com o sentido usual de acrescentar e retirar.

FONTE https://www.todamateria.com.br/adicao/ 

2ºB - ADIÇÃO I

 Juntar, unir e acrescentar são ações que realizamos ao somar.

A adição é uma das principais operações matemáticas, ela está associada à ideia de juntar ou agrupar elementos de conjuntos. Podemos também, com base nela, definir as operações de subtração e multiplicação. Além disso a operação de adição é bastante utilizada em nosso cotidiano, por exemplo, quando vamos ao supermercado, assim, é muito importante compreender sua ideia e o método de como realizá-la.

O que é adição?

A ideia de adição está ligada ao conceito de juntar elementos de dois ou mais conjuntos. Por exemplo, considere o conjunto formado por círculos e o conjunto formado por triângulos.

Agora imagine que nosso interesse seja determinar a quantidade total de figuras geométricas, para isso teremos que juntar os círculos com os triângulos. Quando realizamos esse processo, estamos somando a quantidade de círculos com a quantidade de triângulos, e indicamos essa soma com o símbolo +.

Juntando os elementos dos dois conjuntos temos:

Observe o número de elementos em cada um dos conjuntos, temos 4 (quatro) círculos e 2 (dois) triângulos. Veja também que, ao juntar esses elementos, obtivemos um total de 6 (seis) figuras geométricas, podemos sintetizar todo esse raciocínio em uma expressão matemática, veja:

4 + 2 = 6

Como realizar uma adição?

Veja que o processo de representar graficamente cada elemento da adição torna-se complicado quando colocamos números maiores. Por exemplo, para determinar a soma de 1500 com 1432, teríamos que desenhar 1500 unidades e, em seguida, 1432 unidades, para, assim, contar a quantidade total delas. Veremos, a seguir, um método que facilita esse processo.

Exemplo 1

Determine a soma entre 1500 e 1432.

Para determinar a soma entre os números, devemos primeiramente “armar” a operação. Esse processo consiste em colocar um número sob o outro de maneira que as unidades do primeiro número fiquem sob as unidades do segundo, assim como as dezenas do primeiro número devem ficar sob as dezenas do segundo, e assim sucessivamente. Veja:

Agora, para determinar o valor da adição, basta somar, termo a termo, os valores da tabela anterior, isto é, somar unidade com unidade, dezena com dezena, e assim por diante.

0 + 2 = 2 → Unidade

0 + 3 = 3 → Dezena

5 + 4 = 9 → Centena

1 +1 = 2 → Unidade de Milhar

Assim podemos dizer que 1500 + 1432 = 2932. Podemos simplificar a escrita do processo de adição excluindo a tabela e a escrita das ordens, veja:

Exemplo 2

Determine a soma entre os números 5854 e 4217.

Novamente o primeiro passo é armar a operação entre os dois números.

Somando então termo a termo temos:

4 + 7 = 11 → Unidades

5 + 1 = 6 → Dezenas

8 + 2 = 10 → Centenas

5 + 4 = 9 → Unidade de Milhar

Ao somar termo a termo, observe que a soma das unidades ultrapassa sua capacidade, assim como a soma das centenas, quando isso ocorre, devemos acrescentar o que foi ultrapassado ao termo da próxima ordem.

Portanto devemos acrescentar 1 dezena à casa das dezenas, retirando-a das unidades, e acrescentar uma 1 unidade de milhar à casa das unidades de milhar, retirando-a da casa das centenas, veja:

4 + 7 = 11 – 10→ Unidades

5 + 1 = 6 + 1 → Dezenas

8 + 2 = 10 – 10→ Centenas

5 + 4 = 9 + 1→ Unidade de Milhar

Logo: 5854 + 4217 = 10.071.

Existe também uma maneira simplificada de realizar esse procedimento, basta subir o número que passa em cada casa para a casa da ordem seguinte, veja:

Exemplo 3

Arme e efetue a adição entre os números 6432 e 9993.

Veja que cada aparição do número 1 em cima dos números 4 e 6 representa, respectivamente, a centena e a unidade de milhar que se ultrapassaram.

fonte site escolakids

Vejamos o seguinte probleminha:

“Um grupo de amigos de uma sala de aula se reuniu para comprar um videogame, contudo os amigos estão na dúvida se o dinheiro de todos eles será suficiente para comprar esse videogame. Sabemos que o brinquedo custa 400 reais e que cada integrante desse grupo possui a seguinte quantia: Lucas – 39 reais; Joaquim – 201 reais; Pedro – 55 reais; Luciana – 105 reais”.

Para sabermos quantos reais esses alunos possuem juntos, devemos somar o dinheiro de todos eles, correto?

Façamos essa soma, colocando centena embaixo de centena, dezena embaixo de dezena e unidade embaixo de unidade.

	Centena	Dezena	Unidade
Lucas		3	9
Joaquim	2	0	1
Pedro		5	5
Luciana	1	0	5

Somando as unidades, teremos:
  39
201 +
  55
105

20 unidades (transformando em 0 unidades e 2 dezenas, subimos o 2 para as dezenas)

2
 39
201 +
  55
105
0

Somando as dezenas teremos 10 dezenas, que equivale a 1 centena e 0 dezenas, então subimos 1 centena para a casa das centenas.

1
  39
201 +
  55
105
00

Somando as centenas teremos 4 centenas.

Sendo assim, a soma do dinheiro dos amigos é dada por:

  39
201 +
  55
105
400 reais.

Ou seja, eles possuem dinheiro suficiente para comprar o videogame.

Por Gabriel Alessandro de Oliveira
Graduado em Matemática

Por Escola Kids

2ºB - CONTAGEM E PRINCÍPIOS DA CONTAGEM

Artigo: A importância da contagem para o desenvolvimento matemático

CLARISSA PEREIRA

O que crianças desta idade fazem é decorar uma sequência de palavras. Mas isso não significa que ela está apropriada da contagem. Pensando no contexto de sala de aula, para avaliarmos se o nosso aluno domina esta habilidade, é preciso considerarmos se ele consolidou os Cinco Princípios da Contagem. Já está muito mais do que provado, através de inúmeros estudos científicos, que o domínio desses princípios é um fator DETERMINANTE para o sucesso da aprendizagem matemática.

Quais são o Cinco Princípios da Contagem?

* Correspondência termo a termo: significa que cada objeto pode ser contado somente uma vez. Os alunos que consolidaram esse princípio, não pulam objetos e nem contam o mesmo mais de uma vez;

https://youtu.be/rDIpKAAERvg?si=cX5yHLLglX0YHlzU

* Ordem estável: a ordem da contagem é sempre a mesma, não muda. Começamos sempre pelo um, depois dois, três, quatro… Crianças que contam um objeto por vez, mas pulam o número (do vinte e um vai para o vinte e três, por exemplo, esquecendo-se do vinte e dois), podem não ter consolidado este princípio; 

https://youtu.be/ELm6VjkRmTE?si=30iPTqamyTkQUtD5

* Cardinalidade: significa que o último número de uma contagem indica o total daquele conjunto (se o último que contei foi o oito, então tenho oito objetos);

https://youtu.be/FEH6bGrULCM?si=O7CuJtg9JZpQg2OH

* Irrelevância da ordem: a ordem da contagem não modifica o valor final. Isso significa que eu posso contar da direita para esquerda, da esquerda para a direita, de cima para baixo, do meio para as pontas… e o total daquele conjunto será sempre o mesmo;

* Abstração: significa que objetos de qualquer natureza podem ser contados, não apenas números.

Normalmente, esses princípios são desenvolvidos por volta dos 5 ou 6 anos, sendo que a irrelevância da ordem e a abstração podem se consolidar mais tardiamente.

Como promover o desenvolvimento dos Princípios de Contagem em sala de aula?

Quando trabalhamos com o desenvolvimento da contagem, temos que ter em mente que precisamos de OBJETIVO e INTENCIONALIDADE. Se for algo “puramente natural”, pode não passar de uma contagem decorada. Para desenvolver os Princípios, é necessário ensino EXPLÍCITO. Vamos então para atividades práticas?

* Contagem de objetos enfileirados;

* Contagem dos mesmos objetos, mas dispostos de modo diferente (perguntar se o total mudou);

* Contagem dos mesmos objetos em direções diferentes (dar-se conta que o valor final é sempre o mesmo);

* Tiramos ou acrescentamos um e perguntamos “quantos tem agora? Será preciso recontar tudo novamente?”;

* Ensinamos que não precisa contar desde o início, que podem contar de onde pararam (“a partir de…”);

* Dar objetos enumerados e pedir que as crianças coloquem na ordem correta;

* Tirar um número da sequência e pedir que coloque no lugar certo;

* Jogar jogos se trilhas, jogos de varetas (objetos não numerados que podem ser contados e terem valores diferentes, como no caso das varetas, onde cada cor remete a um valor).

2ºB - SISTEMA DE NUMERAÇÃO DECIMAL

 Será que os homens das cavernas contavam como nós contamos? Será que quando eles caçavam, marcavam uma trilha ou pensavam no tempo, eles imaginavam, escreviam e falavam o número “1, 2, 3…”? Será que faziam agrupamentos de 10 em 10? Certamente não…

Existem diferentes sistemas de numeração (e essa história pode ser trabalhada com as crianças, a fim de que eles compreendam e vejam sentido no nosso sistema!). E, voltando aos homens das cavernas: não temos registros tão antigos de  quantidades nos números que conhecemos hoje, embora existam registros de “risquinhos” que, provavelmente, remetam à contagem. A construção do sistema de numeração decimal não foi feita da noite pro dia, e essa mesma construção nas crianças também leva tempo.

O nosso sistema é decimal porque dizemos que ele tem a base dez. Possuímos 10 algarismos (de 0 a 9) e, com eles, conseguimos construir qualquer outro número. É FUNDAMENTAL que as crianças tenham consolidado bem esse sistema para que possam manipular os números, compreender quantidades e realizar cálculos.

É possível trabalhar com a construção deste sistema desde a Educação Infantil. No primeiro ano, é imprescindível o uso de materiais concretos e manipuláveis, que são próprios para desenvolver essa habilidade. Os materiais mais conhecidos são o ábaco e o material dourado.

Eu,   particularmente, sempre trabalhei com o material dourado e obtive muito êxito. Já fiz uso tanto em sala de aula, como em atendimentos particulares (com crianças que não usavam na escola e conseguiram aprender com facilidade através do material concreto). Se as crianças estão em uma escola que não possui esse recurso, e nem as famílias, o material pode ser confeccionado com E.V.A ou um papel grosso, bem durável. A ideia é que cada um tenha o seu e que eles possam usar o ano todo, afinal, esse material vai servir também para introduzir todos os cálculos.

Como desenvolver o sistema de numeração decimal através do material concreto?

Aí vão algumas dicas:

• Deixar que as crianças manipulem, ainda sem saber pra quê o material serve. Deixar que eles criem hipóteses;
• Manipular como um brinquedo, fazendo construções;
• Começar pelo conceito de UNIDADE, onde cada quadradinho representa UMA unidade;
• Pedir que eles representem quantidades (“quero que cada um, na sua mesa, represente o número 7! Agora o 9!”…). Fazer o registro através de desenhos – damos o número e eles fazem a representação gráfica e também vice-versa;
• Partir para o conceito de dezena (“quantos quadradinhos vamos precisar para montar uma barrinha? Toda vez que eu precisar do 10, posso pegar direto a dezena! Vamos montar o 12? E o 15, como seria? Um desafio: quero que montem o 20…”). A representação gráfica pode (e deve) ser feita novamente como forma de registro;
• Se for o momento, fazer a introdução das centenas da mesma forma;
• Introduzir adição e subtração (“Montem o 18 pra mim! E agora, se tiramos 5, com quantos ficamos? E se colocarmos 3, quanto fica?”);
• Ensinar EXPLICITAMENTE que podemos contar de 10 em 10, de 100 em 100… (“Se eu tenho 8 dezenas, vou contar quadradinho por quadradinho? Não seria muito cansativo? Como posso fazer isso?);
• Trabalhar com o QVL (Quadro Valor Lugar).

FONTE: https://clarissapereira.com.br/sistema-de-numeracao-decimal/ 

2ºB - PROGRAMA

Objetos do Conhecimento

 MATEMÁTICA

▪ Elaboração de aulas seguindo o formato construtivista;

▪ Promoção situações teórico-práticas de acordo com os conteúdos relacionados aos descritores da BNCC.

Habilidades

Compreender o Sistema de Numeração Decimal;

Compreender os conceitos da Adição e da Subtração;

Compreender as operações com números naturais;

Analisar o algoritmo da adição e da subtração

Analisar o algoritmo da Multiplicação e da Divisão;

Analisar diferentes formas e figuras geométricas;

Compreender o ensino de frações nas séries iniciais;

Analisar os sentidos das medidas;

Compreender a leitura de gráficos.

 Analisar o tratamento dado às informações no dia a dia;

Mediar à prática pedagógica na sala de aula para consolidar os conceitos teóricos

por meio da experimentação.